SECODA resources for R

This page presents information taken from Foorthuis (2017) and Foorthuis (2020) on general purpose anomaly detection and high-density anomaly detection.

In statistics and data science, anomalies (or outliers) are cases that are in some way awkward and do not appear to fit the general pattern(s) present in the dataset.

This page offers short descriptions and zip-files with datasets and code to analyze general anomalies and high-density anomalies:

• A. The SECODA algorithm for the detection of anomalies: SECODA is a general-purpose algorithm for detecting various types of anomalies. An implementation for R and various example datasets can be downloaded as a zip-file. The file contains several implementations of SECODA: as an R package, as a code file, and as code file that only uses base R (this code does not use the data.table package and consequently runs slower). The SECODA algorithm is described in Foorthuis (2017).
• B. The IPP and HMDH frameworks for the detection of high-density anomalies: The IPP (Iterative Partial Push) and HMDH (Harmonic Mean Detection of HDAs) frameworks detect high-density anomalies. These are deviating cases in the most dense (or normal) regions of the data. The zip-file offers SECOHDA implementations, which use SECODA as the underlying algorithm, but also implementaitons that use nearest neighbor and LOF based algorithms. The topic of high-density anomalies and the algorithmic frameworks to detect them are described in Foorthuis (2020).

A. The SECODA algorithm for the detection of anomalies:
SECODA is a general-purpose unsupervised non-parametric anomaly detection algorithm for datasets containing continuous and/or categorical attributes. The algorithm is able to detect multiple types of anomalies. The method, in its standard mode, is guaranteed to identify cases with unique or rare combinations of attribute values. SECODA uses the histogram-based approach to assess the density. The concatenation trick - which combines discretized continuous attributes and categorical attributes into a new variable - is used to determine the joint density distribution. In combination with recursive discretization this captures complex relationships between attributes and avoids discretization error. A pruning heuristic as well as exponentially increasing weights and arity are employed to speed up the analysis. See the references below for more information.

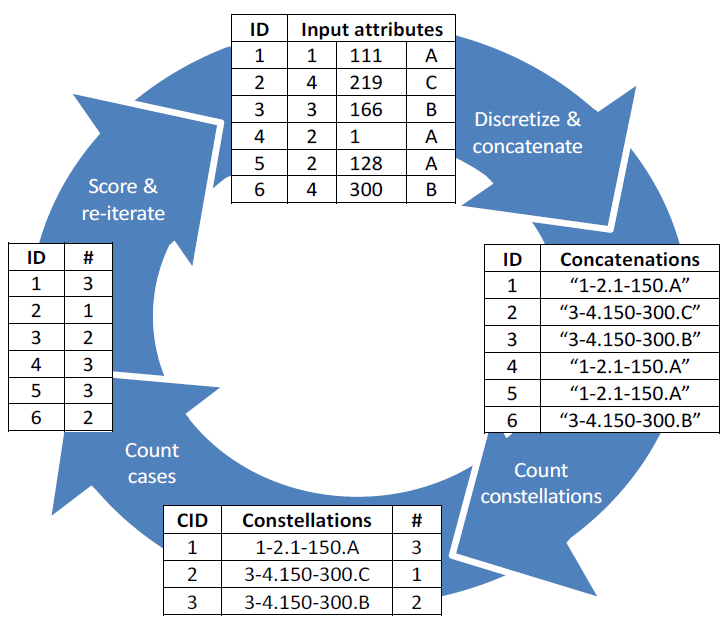
Some characteristics of SECODA:

• It is a simple algorithm without the need for point-to-point calculations. Only basic data operations are used, making SECODA suitable for sets with large numbers of rows as well as for in-database analytics.
• SECODA is able to deal with all kinds of relationships between attributes, such as statistical associations, interactions, collinearity and relations between variables of different data types.
• The pruning heuristic, although simple by design, is a self-regulating mechanism during runtime, dynamically deciding how many cases to discard.
• The exponentially increasing weights both speed up the analysis and prevent bias.
• The algorithm has low memory requirements and scales linearly with dataset size.
• For extremely large sets a longer computation time is hardly required because additional iterations would not yield a meaningful gain in precision. In addition, when analyzing large sets the time performance and precision can be tuned by using less or more iterations.
• Missing values are automatically handled as one would functionally desire in an AD context, with only very rare missing values being considered anomalous.
• Duplicate cases can simply be processed (and thus do not have to be deleted, as opposed to various other anomaly detection algorithms that otherwise will break down).
• The algorithm can be easily implemented for parallel processing architectures.
• In addition, the real-world data quality use case and the simulations not only show that all types of anomalies can be detected by SECODA, but also that they can be encountered in practice.

B. The IPP and HMDH frameworks for the detection of high-density anomalies:
The IPP (Iterative Partial Push) and HMDH (Harmonic Mean Detection of HDAs) frameworks detect high-density anomalies. These are deviating cases in the most dense (or normal) regions of the data. The topic of high-density anomalies and the algorithmic frameworks to detect them are described in Foorthuis (2020).

Sources:
Foorthuis, R.M. (2020). Algorithmic Frameworks for the Detection of High-Density Anomalies. Accepted for presentation at IEEE SSCI CIDM 2020 (Symposium on Computational Intelligence in Data Mining), December 2020, Canberra Australia.
Foorthuis, R.M. (2017). SECODA: Segmentation- and Combination-Based Detection of Anomalies. In: Proceedings of the 4th IEEE International Conference on Data Science and Advanced Analytics (DSAA 2017), Tokyo, Japan.
Foorthuis, R.M. (2017). Anomaly Detection with SECODA. IEEE DSAA 2017 Poster Presentation (DSAA 2017), Tokyo, Japan.
Foorthuis, R.M. (2017). The SECODA Algorithm for the Detection of Anomalies in Sets with Mixed Data.pdf.
Foorthuis, R.M. (2018). The Impact of Discretization Method on the Detection of Six Types of Anomalies in Datasets. In: Proceedings of the 30th Benelux Conference on Artificial Intelligence (BNAIC 2018), November 8-9 2018, Den Bosch, the Netherlands.
Foorthuis, R.M. (2018). A Typology of Data Anomalies. In: Proceedings of the 17th International Conference on Information Processing and Management of Uncertainty in Knowledge-Based Systems (IPMU 2018), Cádiz, Spain.
Page about the Typology of anomalies: Typology.